Mécanisme d’abstraction #
Ce que vous allez apprendre #
Les interfaces sont très utiles pour abstraires des détails techniques. La citation ci-dessous peut être interprétée par “Une bonne architecture est celle qui permet de reporter le plus tard possible les décisions importantes”. Jusqu’à maintenant, nous avons déjà fait la promotion d’une conception basée sur le comportement (le quoi) plutôt que sur les détails d’implémentation (le comment).
A good architecture allows major decisions to be deferred. (Robert C. Martin, Clean Code)
Les interfaces et leur concept de spécialisation/généralisation (héritage), permettent de renforcer cette idée. Une référence r qui respecte une interface I peut être utilisée sans se soucier du choix d’implémentation : elle généralise une utilisation. Cette référence r doit pointer sur un objet d’une classe C, tel que C hérite (ou respecte) I. Nous disons de C qu’elle se spécialise ; elle se préoccupe de mettre en oeuvre les fonctionnalités exigées par I.
Etude de cas : les collections #
Prenons l’exemple des listes. La déclaration List<Integer> is = new ArrayList<>(); est un exemple très concret. La référence is est de type List<Integer> ; List est une interface alors que ArrayList est une classe. Elle indique par une partie de son nom (Array) que c’est une liste réalisée à l’aide d’un tableau statique. Nous aurions pu utiliser une autre stratégie : List<Integer> is = new LinkedList<>();. Nous pouvons manipuler is de la même manière, mais cette fois-ci, le choix s’est porté sur une liste chaînée (Linked).
Pour comprendre l’intérêt, imaginons une méthode réalisant un échange entre les deux premiers éléments d’une liste si celle-ci est composée au moins de deux éléments. Nous avons besoin de supprimer le premier élément de la liste pour l’ajouter en seconde position.
Regardons la hiérarchie des listes. Toutes deux, ArrayList et LinkedList sont des classes qui respectent l’interface List. Cette dernière hérite de Collection qui elle, hérite de Iterable. Le diagramme ci-dessous propose un extrait simplifié des méthodes offertes par chaque type.
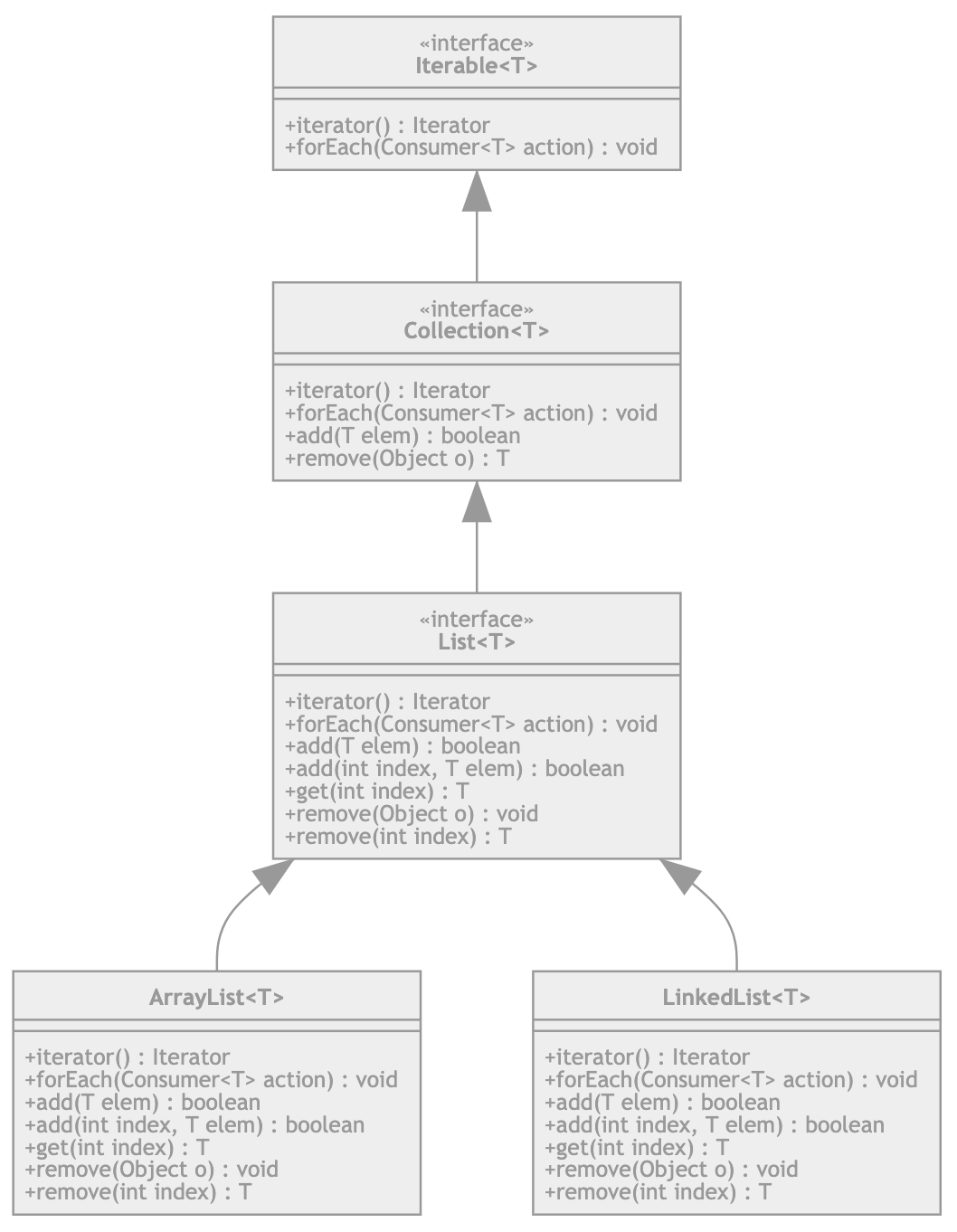
hiérarchie des listes
Nous pouvons déduire que pour supprimer un élément à l’indice 0 pour l’insérer ensuite à l’indide 1, l’interface List est le niveau le plus haut qui nous permet d’effectuer ces deux tâches : la méthode add(T elem) de Collection n’est pas suffisante; elle n’indique pas où sera inséré l’élément. Selon la mise en oeuvre, l’insertion peut se faire au début, à la fin ou arbitrairement selon qu’il s’agit d’une liste chaînée, d’un ensemble, d’une queue de priorité…
Nous pouvons offrir à l’utilisateur une méthode qui prend donc une liste ; il aura le choix de passer n’importe quel type de liste.
|
|
L’utilisateur a la souplesse de changer à tout moment sa stratégie :
- cas de l'
ArrayList:
|
|
- cas de la
LinkedList:
|
|
Vous l’aurez compris, l’avantage est de garder un code-métier générique. Nous restons tolérants sur ce que nous acceptons. Cette technique est apparentée au patron de conception Stratégie (Stretegy Pattern) ou encore à l’injection de dépendaces.
Etude de cas : les tableaux associatifs #
Les tableaux associatifs sont appelés Map en Java. Certains langages les appellent des dictionnaires. Ils permettent de mettre en correspondance des clés avec des valeurs. Une Map ne peut contenir plusieurs fois la même clé.
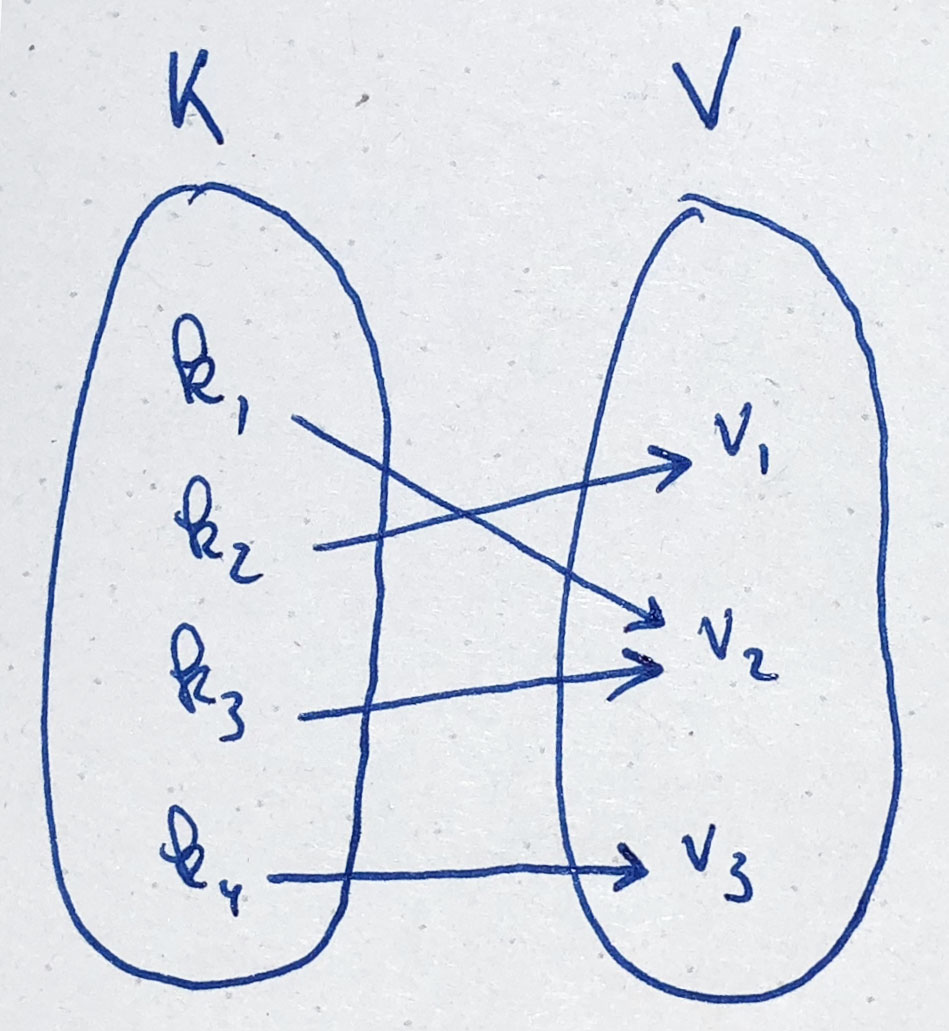
Mapping K/V
Pour chaque clé est associée une valeur, une même valeur peut par contre correspondre à plusieurs clés différentes. Un tableau associatif a également une abstraction définie à l’aide d’une interface Map<K,V> qui est paramétrique. Il faut indiquer le type de la clé (K) et le type de la valeur (V) :
Map<String, String> codeAita = ...
/* le code AITA sont des codes à trois lettres qui désignent
les aéroports internationaux et régionaux */
Plusieurs spécialisations sont proposées sous formes de classes. Les plus connues sont :
HashMap<K,V>- mise en oeuvre à l’aide d’une table de hachage
- la clé doit redéfinir les méthodes
hashCode()/equals()
TreeMap<K,V>- mise en oeuvre à l’aide d’un arbre équilibré
- implémente également l’interface
SortedMap<K,V> - la clé doit redéfinir la méthode
equals() - la clé doit implémenter l’interface
Comparable<T>(ou alors, il est nécessaire de passer unComparatorau constructeur)
Instanciation:
Map<String, String> aita = new HashMap<>();
// ou
Map<String, String> aita = new TreeMap<>();
Exemples d’utilisation:
|
|
Un tableau associatif peut être représenté à l’aide d’une liste de couples (clé, valeur) :
[
(LHR, Londres Heathrow),
(GVA, Aéroport international de Genève),
(ORY, Aéroport de Paris-Orly)
]
Quiz #
Nous souhaitons parser un fichier et compter le nombre d’occurrences de chaque mot.
- Quelle serait la déclaration d’un tableau associatif permettant de réaliser cette tâche ?
- Puis, connaissant un mot, quelle est l’opération permettant d’incrémenter son nombre occurrence ?
Conclusion #
Pour conclure, l’abstraction permet d’encourager le principe “code pour une interface et non pour une implémentation”. Il permet de décrire le comportement que devrait avoir un module plutôt que de s’intéresser trop tôt à comment le mettre en oeuvre.
Une analogie est un composant physique qui nécessite de l’électricité. Nous ne souhaitons pas que notre composant ait une dépendance vers une source spécifique comme l’illustre l’image suivante :

images: wikipedia
Au contraire, nous ne voulons pas nous soucier des détails, nous souhaitons une abstraction d’une source d’énergie que l’on représenterait par une prise murale :
